統計学はAI開発の基礎です。データサイエンスには統計学が使用されます。
また、データサイエンスに限らずとも、様々な数字を統計学を使用し分析することは、ITの得意とすることの一つです。
この記事では、そんな統計学のPythonでの記述方法について、基本的な事柄を解説します。
はじめに
統計量の処理には、NumpyとScipyを使用します。
Numpyは数値処理のライブラリ、Scipyは数値解析のライブラリです。
Numpyが基本処理、Scipyが応用処理と覚えておけばほぼ合っています。
以下の文でimportします。
import numpy as np import scipy
一般的に、Numpyの関数は
np.~
と記述して使用します。
平均
平均はデータを全て足し、データの個数で割ったものです。
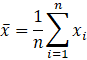
という数式で計算できます。
Numpyのmean関数で計算できます。引数に数の配列を与えます。
>>> import numpy as np >>> values = [2, 3, 5, 9, 1] >>> np.mean(values) 4.0
中央値
中央値はデータをソートして並べた時に真ん中に来る値です。
Numpyのmedian関数で計算できます。
>>> import numpy as np >>> values = [2, 3, 5, 9, 1] >>> np.median(values) 3.0 >>> values.append(1) >>> np.median(values) 2.5
最初のvaluesをソートしたとき、中央に来るのは3ですね。
valuesの個数が偶数だった場合、中央付近の2つの数の平均値になっています。
分散
分散は言葉で説明するとややこしいので、まず数式を見てください。
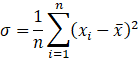
平均を使って計算します。
この数式から分かる通り、「平均から各数値がどれくらい離れているか」を集計するのが分散です。
平均から離れている数値が多いほど分散は大きくなります。逆に、平均付近に数値が集まっていれば、分散は小さくなります。
Numpyのvar関数で計算できます。
>>> import numpy as np >>> values = [2, 3, 5, 9, 1] >>> np.var(values) 8.0 >>> values = [2, 3, 5, 4, 4] >>> np.var(values) 1.0400000000000003
標準偏差
標準偏差は分散の平方根です。
Numpyのstd関数で計算できます。
>>> import numpy as np >>> values = [2, 3, 5, 9, 1] >>> np.std(values) 2.8284271247461903 >>> values = [2, 3, 5, 4, 4] >>> np.std(values) 1.019803902718557
分散の数値の平方根になっていることが分かりますね。
共分散
二つの統計量x,yの共分散とは、以下の式で求められます。
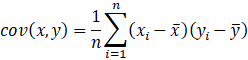
これもまた「平均からの差の積の平均」ですから、ばらばらであるほど共分散は大きくなります。まとまっていれば大きくなりません。
Numpyのcov関数で共分散行列が計算できます。
共分散行列は以下のような構造をしています。
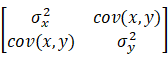
この行列の
1行2列
か
2行1列
がもとめる共分散です。
>>> import numpy as np
>>> xs = [2, 5, 9, 1, 3]
>>> ys = [1, 3, 0, 1, 2]
>>> np.cov(xs, ys, ddof=0)
array([[ 8. , -0.8 ],
[-0.8 , 1.04]])
ddof=0とは、共分散の計算時に、単純にデータの個数で割るための指定です。
相関
次に、二つの統計量x,yの相関とは、以下の式です。
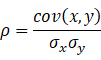
共分散を解釈しやすくしたものです。
Numpyのcorrcoef関数で相関行列が求められます。
相関行列は以下の形をしています。
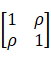
先ほど求めたxs、ysに対し、相関を計算すると、
>>> import numpy as np
>>> xs = [2, 5, 9, 1, 3]
>>> ys = [1, 3, 0, 1, 2]
>>> np.corrcoef(xs, ys)
array([[ 1. , -0.2773501],
[-0.2773501, 1. ]])
となります。
正規分布
確率分布とは、「それがどのくらいの確率で現れるかの分布」です。
正規分布とは、その中でも代表的な確率分布で、統計量の母数を多くしていくとこの分布に従うことが多いです。
正規分布の値は、xに対し以下の式で求められます。
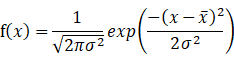
この式は、scipy.statsモジュールに用意されています。
norm.pdf(x,loc,scale)
です。
locは平均、scaleは標準偏差を与えます。
norm.pdfを利用して、正規分布の式のグラフを書いてみます。
loc = 0
scale = 1
として、
-10
から
+10
まで書いてみましょう。
コードは以下となります。
import matplotlib as mpl
mpl.use('Agg')
import matplotlib.pyplot as plt
from scipy.stats import norm
import numpy as np
xs = np.linspace(-10, +10, 201)
ys = []
for x in xs:
ys.append(norm.pdf(x, 0, 1))
plt.plot(xs, ys)
plt.savefig("正規分布.png")
結果のグラフは
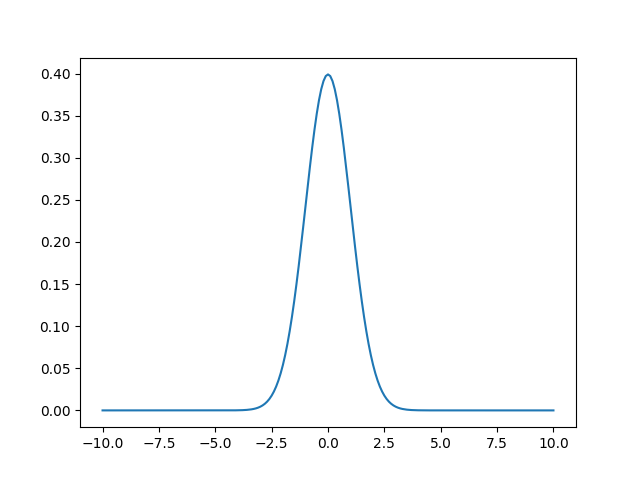
np.linspace
は、区間の間の数値の配列を作る関数です。
すそ野が大きく広がっていますが、値は0ではありません。0に近いですが。
このような分布を統計量はとります。
まとめ
この記事では以下の統計の基本量の求め方を見てきました。
- 平均
- 中央値
- 分散
- 標準偏差
- 共分散
- 相関
また、以下の関数について紹介しました。
- 正規分布
これらはいずれも、統計学で基礎となるものです。
しかしいずれもPythonを使えば簡単に求めることができました。
Pythonが統計処理に適している言語だということが理解していただけたかと思います。
Pythonの簡潔な記述は統計処理のような複雑な計算を楽にしてくれます。
NumpyやScipyに用意されているものなので、自分で計算処理を書かずにNumpyやScipyを使うようにしましょう。